The Change of the Shape of Earthã¢â‚¬â„¢s Orbit From Circular to Elongated and Back Again:
ii Chapter 2 – Orbit Geometry
ORBITS AS CONIC SECTIONS
In Chapter 1, the Ii Body Equation of Motility was developed and we discussed how the elliptical orbit was one possible solution. However, in general the solution can exist whatever of the 4 conic sections: circles, ellipses, parabolas and hyperbolas. We volition start this chapter with a discussion of how a satellite gets into orbit and chronicle it to the conic sections. We will so review the elliptical orbit and its parameters and then extend these results to consider the other conic sections.
Commencement, how does a satellite become into orbit? Imagine y'all are at the top of a mountain and and start firing a cannon from it. We tin can think of the missive as a projectile, an object that, when it is set in move, continues in its path by its ain inertia and is influenced only by the downwards force of gravity. The horizontal motion of the projectile is the event of the tendency of any object in motility to remain in motion at a constant velocity. The vertical motion of the projective, or cannonball, is influenced past the gravitational acceleration, thou, pulling downward. The horizontal and vertical motions are contained, hence, the faster you fire the cannonball, the further it will go. As an instance, attempt the Newton's Cannon simulator beneath. In this simulation, the cannon was fired at 3000 m/s, 4000 k/southward, 5000 chiliad/s and 6000 m/s. Each time the cannonball goes a niggling farther before hitting the earth. Try the simulator yourself and meet what happens! (Schroeder, 2020).
Since the earth is approximately spherically shaped (nosotros will find out later this this information technology not entirely truthful), its surface drops well-nigh 5 meters for every 8 km the cannonball travels horizontally. So, if we fire the cannonball faster and faster (assuming no air resistance), its path would eventually match the charge per unit of curvature of the earth. Here are the results of the simulator firing the cannon at 7300 grand/south, 7600 m/s, and 8000 one thousand/southward. You will notice that at the lower velocity, the orbit is nearly circular; however, equally the cannonball is fired faster and faster, the orbital shape becomes more elliptical. In fact, as more and more than horizontal velocity is added, the orbit will eventually become parabolic, so hyperbolic, somewhen breaking away from the earth'southward sphere of influence entirely. We will consider each of these types of orbits in this affiliate.
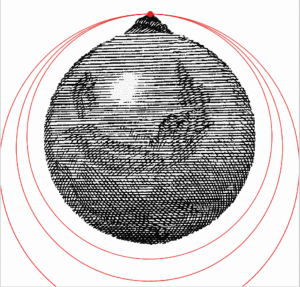
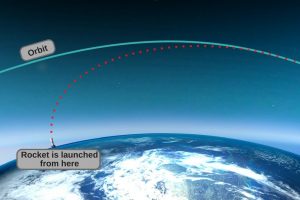
A rocket launches vertically to get as quickly every bit possible out of the earth's thick atmosphere and minimize drag. However, you lot will notice that it begins to tilt horizontally and gradually increases this tilt until it achieves orbit around the earth. This technique of optimizing a trajectory of a rocket and then that it attains the desired path is called a gravity turn. This technique allows the rocket to employ Globe'southward gravity, rather than its own fuel, to change its direction. The fuel that the rocket saves and so be used to accelerate it horizontally in social club to reach loftier speed and more easily enter into orbit.
ELLIPTICAL ORBITS
Kepler's First Law said the orbits of the planets are ellipses. These are the virtually mutual orbits because one object is 'captured' and orbits another larger object. Not only practise the planets and minor planets have elliptical orbits, most comets and binary stars as well do. The velocity in elliptical orbits is always less than that needed to escape from the central object's influence. Allow u.s. have a closer look at the geometry of an orbital ellipse that we considered in Affiliate i and describe each of its parameters more than precisely.
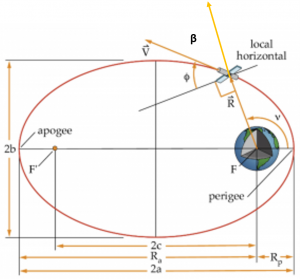
= satellite position vector, measured from the center of the Earth
R is the radius from the focus of the ellipse (center of the earth) to the satellite, or 
, the magnitude of the vector
= satellite velocity vector, tangent to the orbital path
V is the magnitude of the vector
F and F' = chief (occupied) and vacant (unoccupied) foci of ellipse
Rp = Radius of periapsis (closest bespeak) = Radius of perigee when the satellite is around the earth = a(1-e)
Ra = Radius of apoapsis (farthest point) = Radius of apogee when the satellite is effectually the world = a(i+e)
a = semi-major centrality 
b = semi-minor axis
2c is the distance betwixt the foci = Ra – Rp
e = eccentricity, the ratio of the distance betwixt the foci (2c) to the length of the ellipse (2a), or 
. Thus
Eccentricity defines the shape of the conic section. For ellipses,
0 < e < 1
= true anomaly = the polar angle measured from perigee to the satellite position vector, , in the management of satellite motion
= flight path bending, measured from the local horizontal to the velocity vector, .
When the satellite is traveling from perigee to apogee, the velocity vector will ever be above the local horizon (gaining altitude) then >0 for 
When travelling from apogee to perigee, the velocity vector will ever exist beneath the local horizon (losing distance) then <0 for 
.
At exactly apogee and perigee on an ellipse, the position and velocity vectors will exist perpendicular and then the velocity vector is parallel to the local horizon, hence = 0.
p = semi-latus rectum = the magnitude of the position vectors at = 90 degrees and 270 degrees
Since ellipses are closed curves, an object in an ellipse repeats its path over and over. The time for a satellite to go in one case around its orbit is called the period. For a detailed derivation of the period equation, see Bate.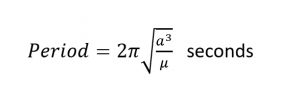
Let u.s.a. review what we know about orbits and so far earlier taking a look at special types of orbits.
- Conic sections are the only possible paths for an orbiting object governed by the ideal two torso equation of movement.
- The focus of the conic department is the center of the central body.
- The specific mechanical energy,
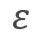is constant, and so potential energy and kinetic energy are traded off co-ordinate to the relationship
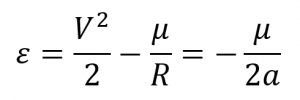
This human relationship likewise tells u.s. that the orbit size is stock-still.
The velocity tin can then be constitute from past rearranging this equation to yield:
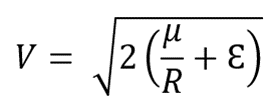
4. The specific angular momentum,
is constant, so the orbital plane is stock-still in orientation. As well
where 
is the angle betweenand so
Call up at at apogee and perigee, and are perpendicular so since = 0 degrees,
h = RpVp
and
h = Ra5a
Finally, from Affiliate one nosotros found another express for specific angular momentum,
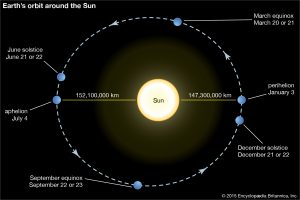
An instance of an elliptical orbit is the Earth's orbit around the sun. It has a semi-major axis, a, of approximately 149,598,260 km and an eccentricity of 0.0174. This is a very low eccentricity, which results in only a iii% difference in the altitude to the sun at perihelion and aphelion.
An example of a highly elliptical earth orbiting satellite is ane travelling in a Molniya orbit (see Figure below). Information technology is a 12-60 minutes orbit with semi-major centrality, a, of 26,571 km, an eccentricity, eastward, of about 0.7. Its perigee is located in the Southern hemisphere and the satellite spends eleven hours, or about 92% of its time, in the northern hemisphere. We will study more about Molniya orbits when we talk over perturbations later in this book.
In the adjacent section, we will consider a special example of elliptical orbits, round orbits. But commencement, work through this example trouble to meet how well you understand the concepts from this section. The answers and solutions are at the cease of this chapter.
EXAMPLE 1
The altitude of a satellite at perigee is 500 km and its orbital eccentricity is 0.1. Detect:
a) The satellite's altitude at apogee
b) The orbit'south specific mechanical free energy,
c) The magnitude of the orbit'due south specific angular momentum, h
d) The satellite'south speed at apogee
CIRCULAR ORBITS
The circular orbit is just a special case of an elliptical orbit so the relationships for an elliptical orbit described above are valid.
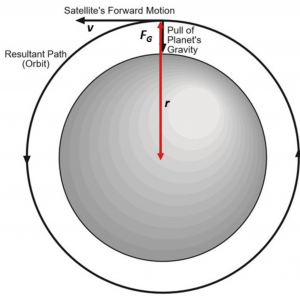
The semi-major centrality, a, is just it'south radius, or a = R and the eccentricity of a round orbit, e = 0. This makes the period equation, in seconds,
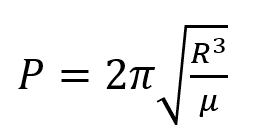
Also notice that the Velocity vector,, is always perpendicular to the Position vector, ,so the flight path angle, is e'er equal to aught. Nosotros can calculate the speed required for a circular orbit of radius R from the velocity equation:
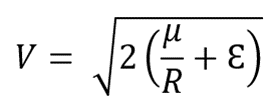
Now we know
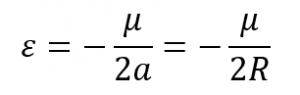
So now
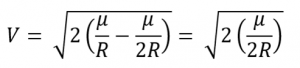
So the velocity of a satellite in a circular orbit simplifies to a abiding:
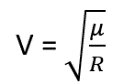
Notice that the greater the radius of the circular orbit, the less speed is required to keep the satellite in this orbit. For a depression altitude earth orbit, the circular speed is nigh 7.eight km/s, while the speed required to keep the moon in its orbit around the earth is only about 0.9 km/s.
Although satellite orbits never have eccentricities exactly equal to zero, in that location are some satellites that come up close. Global Positioning System (GPS) satellites provide navigation services worldwide. The satellite constellation's main functions are to transmit radio-navigation signals, and to store and retransmit navigation messages. These transmissions are controlled past highly stable atomic clocks on lath the satellites. The constellation is designed and then users volition take at least iv simultaneous satellites in view from any point on the World surface at any time. The United Sates is committed to maintaining the availability of at least 24 operational GPS satellites 95% of the time. This means at whatever ane time there are most 30 operational GPS satellites (esa, 2020).
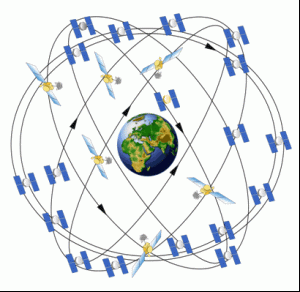
GPS satellites fly in medium space orbit (MEO) at an altitude of approximately 20,200 km, which results in a period of 12 hours and an orbital speed of 3.nine km/s. They are in half-dozen planes spaced equally (sixty degrees autonomously) with four satellites in each. These orbits are nearly round, with eccentricity less than 0.02.
Another case of a nearly round orbit is the one used for the International Space Station (ISS). The ISS is a modular space station, or habitable artificial satellite and is a multinational collaborative projection involving five participating space agencies: NASA (Usa), Roscosmos (Russian federation), JAXA (Japan), ESA (Europe), an CSA (Canada). It serves as a microgravity and space environs research laboratory and has been continuously occupied by humans since November 2000. The ISS flies in Depression Earth Orbit (LEO) at an altitude of approximately 420 km, which results in a period of just over 90 minutes. This means the ISS circles the earth xv to 16 times a twenty-four hours! Its orbit is as well nearly circular, with an eccentricity of 0.0003 and an orbital speed of 7.7 km/s. It is at a relatively high orbital tilt of 51.half dozen degrees relative to earth's equator, resulting in it passing over a large portion of the earth's surface each 24-hour interval.
In the next section, we volition consider parabolic orbits. Only first, piece of work through this example problem to see how well yous understand the concepts from this department. The answers and solutions are at the finish of this chapter.
Instance 2
An geostationary orbit (GEO) is i in which a satellite always remains above the same point on the world's equator. For a GEO satellite, the radial from the center of the globe to the satellite must have the same angular velocity as the earth itself, or a period of 24 hours.
a) Summate the distance of a GEO orbit.
b) Summate the specific mechanical energy, , of a GEO satellite's orbit.
c) Calculate the speed of a GEO satellite.
PARABOLIC ORBITS
Parabolic orbits are rarely institute in use, simply they are important and interesting because they are the borderline case between the elliptical (closed) orbit and the hyperbolic (open up) orbit.
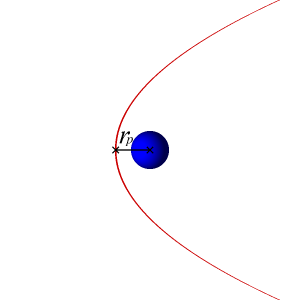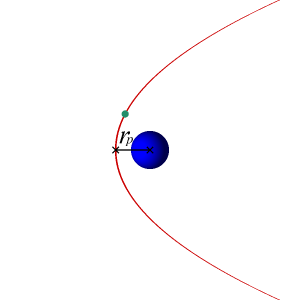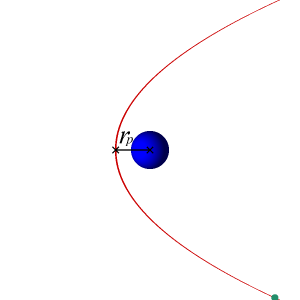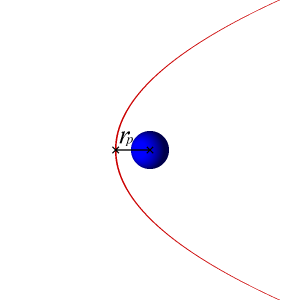
The semi-major axis of a parabolic orbit is infinitely large, so an object traveling in a parabolic orbit is on a i-way trip to infinity and will never retrace the aforementioned path again. A unique property of a parabolic orbit is that the two arms of the parabola become more than and more virtually parallel equally they are extended farther and further to the right of the focus.
Also, since the eccentricity of a parabolic orbit is 1, the radius to perigee equation used for elliptical orbits, Rp = a(1 – e), cannot be used so the more generic form will be used:
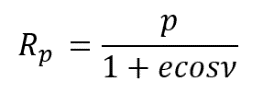
Thus, for e = 1 and = 0 degrees, this becomes:
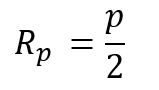
Of course, there is no apogee for a parabola and it may exist thought of equally an infinitely long ellipse.
Even though a planet'south gravitational field strength theoretically extends to infinity, its force decreases rapidly with distance from the heart body such as the globe. Thus, in that location is a finite amount of kinetic energy that is needed to overcome the effects of gravity and allow an object to declension to an "infinite" distance without beingness pulled dorsum toward the globe. The speed at which this occurs is chosen the escape speed, 5esc . Theoretically, as the object's distance from the earth approaches infinity, it's speed approaches zero. This results in a total specific mechanical energy, = 0 for a parabolic orbit.
We tin can then summate the speed necessary to escape by writing the free energy equation for this indicate:
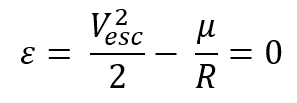
Thus
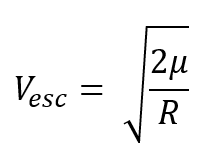
Every bit you would expect, the farther away you lot are from the earth, the less speed it takes to escape from the remainder of the gravitational field. The escape speed from the surface of the earth is most 11.2 km/s, while from a point 6300 km higher up the surface, it will only take most 7.9 km/s.
Although parabolic orbits are not used in practise, some comets approach parabolic orbits. For case, Comet McNaught, also known equally the Great Comet of 2007 and given the designation C/2006 P1, is a non-periodic comet. Information technology was discovered on vii August 2006 by British-Australian astronomer Robert McNaught. It was the brightest comet in over 40 years and it was visible to the naked heart for observers in the Southern Hemisphere in Jan and February 2007. Around perihelium on 12 January, information technology was visible in broad daylight. The comet as seen from Swifts Creek, Victoria, Australia, may be seen below.
Its perihelion is 0.17 Astronomical Units (AU), where one AU is the distance of the earth from the sun, or about 149,597,871 km. This means it came as close as 25,544,000 km to earth. However, with an eccentricity of ane.000019, its aphelion is virtually 4100 AU and it has a period of about 92,600 years! Although we know its last perihelion was in 2007, it is unknown when it will return, or even where humans may be settled in our galaxy that far in the future.
In the side by side section, we will consider hyperbolic orbits. But first, work through this example problem to meet how well yous understand the concepts from this section. The answers and solutions are at the terminate of this chapter.
EXAMPLE iii
A Jupiter probe is in a circular orbit around World with a radius of 25,000 km. The next pace on the way to Jupiter is to thrust so the probe can enter into an escape orbit.
- Decide the probe's velocity in this round orbit.
- Determine the minimum velocity required to enter a parabolic trajectory at that radius.
- Make up one's mind the difference in the specific kinetic, potential, and mechanical energies between the two orbits.
HYPERBOLIC ORBITS
Hyperbolic orbits are very useful, peculiarly for interplanetary travel. An interplanetary probe must take some speed left over afterward information technology escapes the globe'south gravitational field.
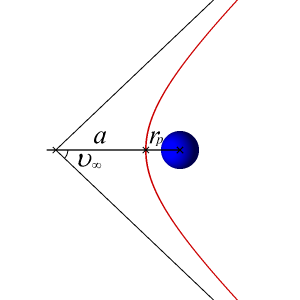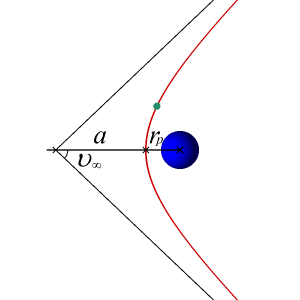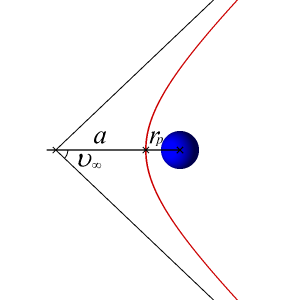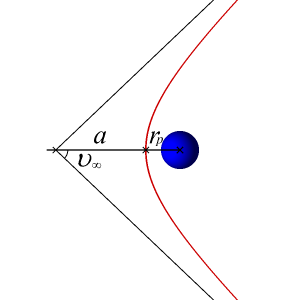
The semi-major axis of a hyperbolic orbit is negative. This seems similar a strange phenomenon, merely information technology makes sense if y'all consider the specific mechanical free energy of a hyperbolic orbit:
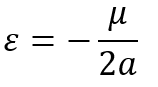
If the semi-major centrality, a, is negative, this volition make the specific mechanical free energy positive. Thus in the energy equation,
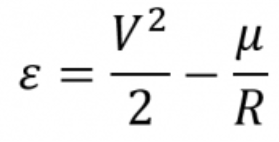
as R gets very large, the potential free energy term gets smaller and smaller, leaving merely kinetic energy!
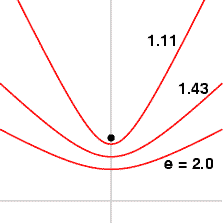
In improver, the eccentricity of a hyperbolic orbit is greater than 1. The eccentricity gets larger the more spread out the arms are. For some examples of how eccentricity is afflicted based on the shape of the hyperbola, meet the figure below. For more details on hyperbolic orbit geometry, meet Bate.
Also, the same form to observe radius of perigee for a parabolic orbit is used, while radius to apogee is infinitely large.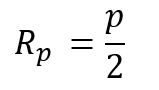
So now allow's consider how hyperbolic trajectories are used for interplanetary travel and some terminology associated with them. If y'all requite a spacecraft exactly the escape speed, information technology volition just barely escape the gravitational field. This means that its speed volition approach zip as its distance from the world approaches infinity. However, if we give our spacecraft more than the escape speed at a signal near the earth, the speed at a keen distance from the globe volition accept some positive value. This rest speed which the spacecraft would have left over is called the "hyperbolic backlog speed, or 
.
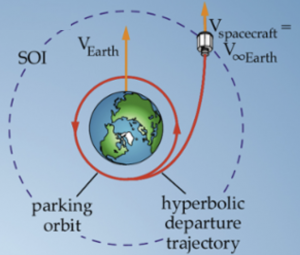
If a satellite starts in a parking orbit near earth, we can notice the speed needed to depart from the parking orbit to achieve at an infinite distance from the earth, which we volition consider the earth'due south Sphere of Influence, or SOI. Although it is hard to notice an agreed-upon definition, for our purposes we tin can consider it approximately 1.5 million km from the earth.
We can then calculate the heave needed to get on the hyperbolic departure trajectory to the edge of the earth's SOI past writing the free energy equation at 2 points on this orbit. The outset point is at the parking orbit, called Burnout Velocity, VBO. The 2nd point will be at the border of the globe's SOI, or . Since:
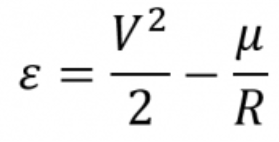
Since the free energy needed at the edge of the earth's SOI, or
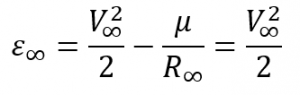
This energy must exist equal to the energy needed to get on the hyperbolic escape trajectory at the parking orbit, or
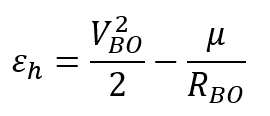
And then
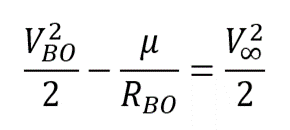
Rearranging this equation yields:
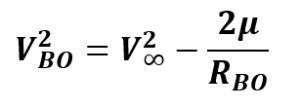
Notice the last term:
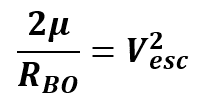
So our last equation relating these velocities become:
Now allow usa recap the meaning of these velocity terms.
VBO = the velocity needed at the parking orbit to achieve the velocity needed at the edge of the Globe's SOI
= the velocity needed at the border of the Earth's SOI to break away from the earth's influence
Vesc = the velocity need to barely get to the Earth's SOI with no excess velocity
Finally, to go from an initial parking orbit (bold circular) to a hyperbolic escape orbit, we must first know the spacecraft'south velocity in the parking orbit:
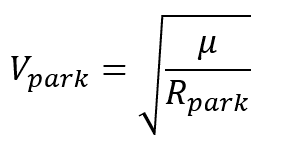
Then
Then the modify in velocity, or boost needed to escape the earth'due south sphere of influence is given by:
Where the vertical lines represent the absolute value of the effect.
Although nosotros do not encounter hyperbolic trajectories much on earth or for earth-orbiting satellites, they are very common in interplanetary travel and amongst bodies in our solar organisation. Meteors that strike the earth travel on hyperbolic paths relative to the globe. The Perseids Meteor Showers are ane instance. These meteors, which peak during mid-August, originate from comet 109P/Swift-Tuttle. Swift-Tuttle is in an elliptical orbit around the sun and has a period of 133 years. Comet Swift-Tuttle last visited the inner solar arrangement in 1992. When it came around the lord's day, it left a dusty trail behind information technology. Every year Earth passes through these debris trails, which allow bits of leftover comet particles to collide with our temper that disintegrate to create fiery and colorful streaks in the sky. At its peak, it tin result in upward to 100 meteors per hour at speeds of approximately 59 km/s (NASA 2019).
Interplanetary missions must utilize hyperbolic trajectories, relative to the globe, if we want the interplanetary probe to intermission abroad from the World'southward gravitational field. An interesting interplanetary spacecraft is New Horizons, which was sent to explore far into our solar system. By the time it reached Pluto, the spacecraft had travelled farther away and for a longer time period, more ix years, than any previous deep space spacecraft ever launched. It observed Pluto shut up, flying by the dwarf planet and its moons in July 2015. (NASA 2020).
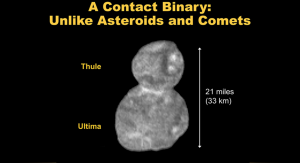
In early 2019, New Horizons flew past its second major science target, 2014 MU69, the most distance object ever explored upwardly close. New Horizons discovered the object is a contact binary, two different spherical objects. The lobes were formed separately an and then eased together over four billion years ago at speeds between 1 to two miles per hr. These ii rocks were and then pulled together past the extremely weak gravitational forces of each other, nudging together at such tiresome speeds that initial observations from New Horizons do not reveal whatsoever stress fractures or harm from the "standoff". More than discoveries by New Horizons are yet to come (Gebhart, 2019).
In society to get on this interplanetary trajectory, New Horizons was launched in January 2006 from Cape Canaveral Air Forcefulness Station. Yous will larn later in this book why the Cape is an ideal location from which to launch an interplanetary probe. It was launched into a hyperbolic departure trajectory that took it on a path by Jupiter. The behemothic planet's gravitational pull helped information technology "slingshot" the spacecraft toward the outer solar system.
In that location are two reasons why the New Horizons scientific discipline team wanted to attain Pluto as shortly as possible. The starting time had to practise with Pluto's atmosphere: Since 1989, Pluto has been moving further from the Sun, getting less heat every year. Every bit Pluto gets colder scientists expect its atmosphere volition "freeze out," so the squad wanted to make it while there was a chance to written report a thicker temper.
The second reason was to map as much of Pluto and its largest moon, Charon, as possible. On World, the North Pole and other areas above the Arctic Circle have half a year of night and half a year of daylight. In the same way, parts of Pluto and Charon never see the Sunday for decades at a time. The longer the look, the more of Pluto and Charon would have been shadowed in a long "chill nighttime," impeding the spacecraft'due south ability to accept pictures of the surface in reflected sunlight.
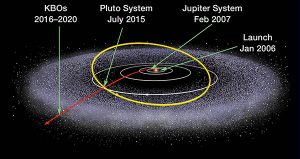
In February 2007, New Horizons passed through the Jupiter system at more than than fifty,000 mph, ending upward on a path that got information technology to Pluto on July 14, 2015, nearly nine and a half years after versus the 30 years or and then information technology would take to get there directly. The figure below shows the path New Horizons took to get to Jupiter and the Kuiper Belt Objects (KBOs) You will larn most gravitational help trajectories later. Without the use of hyperbolic trajectories, however, New Horizons would take never left World's gravitational field at all!
Now, piece of work through this example trouble to run into how well you sympathize the concepts from this section. The answers and solutions are at the end of this chapter.
EXAMPLE iv
A spacecraft is launched from a parking orbit around earth to Mars.
Given:
= 2.94 km/s
RPark_at_Earth = 6697 (circular)
Find:
a) 
energy needed at the edge of the Earth's sphere of influence
b) VBO = the velocity needed at the parking orbit to achieve the velocity needed at the edge of the World's SOI
c) 
needed= The boost needed to become the spacecraft from its parking orbit onto the hyperbolic departure trajectory
SUMMARY
In this chapter, nosotros commencement discussed how a satellite gets into orbit and related it to the conic sections. We then reviewed elliptical orbits and its parameters, so extended these results to consider the other conic sections. Below is a summary of the orbits types and the value or range of values for some of their orbital parameters.
| Orbit Type | Semi-major axis, a | eccentricity, eastward | Specific mechanical energy, |
| Ellipse | a > 6578 km* | 0 < due east < 1 | < 0 |
| Circle | a = R (constant) | e = 0 | < 0 |
| Parabola | a =  | e = i | = 0 |
| Hyperbola | a < 0 | e > 1 | > 0 |
* World's radius + 200 km
Check your understanding with this quick quiz!
SOLUTIONS TO EXAMPLES
Example 1
The altitude of a satellite at perigee is 500 km and its orbital eccentricity is 0.1. Observe:
a) The satellite's altitude at apogee
Since
Rp = a(1-e)
6378 km + 500 km = a(1-0.1)
a = 6878/0.9 km
a = 7642 km
and
Ra = a(1+e) = 7642(i+0.1)
Ra = 8406 km
So the satellite's altitude at apogee = 8406 – 6378 km
Altitude at apogee = 2028 km
b) The orbit's specific mechanical energy,
Since
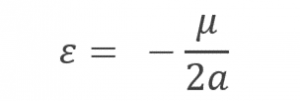
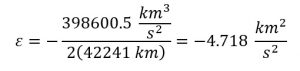
so
= -26.08 kmtwo/south2
c) The magnitude of the orbit'south specific athwart momentum, h
Since
so
h = 54915 kmtwo/s
d) The satellite'south speed at apogee
Since h = RaVa
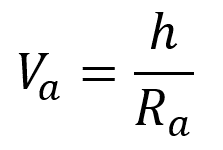
so
5a = 6.53 km/s
Example 2
An geostationary orbit (GEO) is one in which a satellite always remains in a higher place the same bespeak on the earth'southward equator. For a GEO satellite, the radial from the center of the earth to the satellite must have the same angular velocity as the world itself, or a period of 24 hours.
a) Calculate the altitude of a GEO orbit.
Since
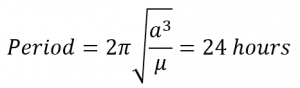
So
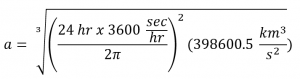
a = 42241 km
altitude of a GEO satellite = 35,863 km
b) Summate the specific mechanical energy, , of a GEO satellite's orbit.
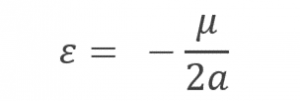
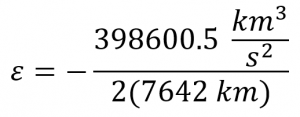
= -4.718 km3/due south2
c) Calculate the speed of a GEO satellite.
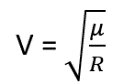
so
V = iii.07 km/due south
Example 3
A Jupiter probe is in a circular orbit effectually Earth with a radius of 25,000 km. The next step on the way to Jupiter is to thrust so the probe can enter into an escape orbit.
- Determine the probe'southward velocity in this round orbit.
Since R = 25,000 km
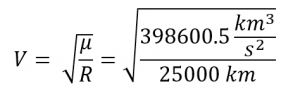
And so
V = three.99 km/s
2. Determine the minimum velocity required to enter a parabolic trajectory at that radius.
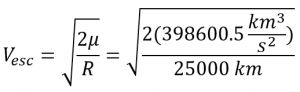
So
Five = five.65 km/s
three. Decide the difference in the specific kinetic, potential, and mechanical energies between the two orbits.
Orbit 1 (round parking orbit)
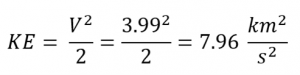
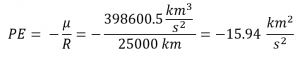
= -7.98 km2/stwo
Orbit two (Escape Orbit)
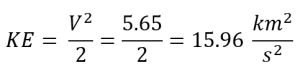
= 0
So PE doesn't change (any small departure is due to circular-off error) while KE changes past 8 km2/s2. Since the Specific Mechanical Energy changes by approximately 8 km2/southii, all of the free energy added is strictly due to the alter in KE.
EXAMPLE 4
A spacecraft is launched from a parking orbit around earth to Mars.
Given:
= ii.94 km/s
RPark_at_Earth = 6697 (circular)
Find:
a) energy needed at the edge of the World'due south sphere of influence
= 0.five * (2.94 km/s)2
= iv.32 km2/stwo
b) 5BO = the velocity needed at the parking orbit to accomplish the velocity needed at the edge of the Globe's SOI
So
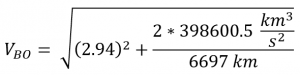
VBO = 11.three km/due south
c) = The heave needed to get the spacecraft from its parking orbit onto the hyperbolic difference trajectory
The satellite's velocity in its original parking orbit is
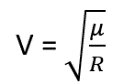
and then
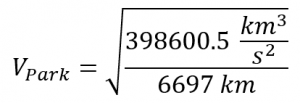
Fivepark = 7.71 km/s
and
And then
= 3.585 km/s
REFERENCES
American Mathematical Lodge. (2005).Sling Shots and Space Shots. http://world wide web.ams.org/publicoutreach/characteristic-column/fcarc-slingshot.
Ashish. Why practice rockets follow a curved path instead of going straight into space? (2021, iii Feb). https://www.scienceabc.com/nature/universe/why-do-rockets-follow-a-curved-trajectory-while-going-into-infinite.html
Bate, R. R., Mueller, D. D., White, J. East., & Saylor, W. W. (1971). Fundamentals of astrodynamics. Mineola (Due north.Y.): Dover Publications.
Britannica. Orbit. (2021). https://www.britannica.com/science/orbit-astronomy
European Space Agency navipedia. (2020, 20 Nov). GPS Space Segment. https://gssc.esa.int/navipedia/index.php/GPS_Space_Segment
Gebhardt, W. (2019, January 02). 2014 MU69 Revealed as a Contact Binary in Kickoff New Horizons Data Returns. https://world wide web.nasaspaceflight.com/2019/01/2014-mu69-contact-binary-outset-new-horizons-returns/
NASA Solar Organization Exploration. (2019, 19 December). Perseids: In Depth.https://solarsystem.nasa.gov/asteroids-comets-and-meteors/meteors-and-meteorites/perseids/in-depth/
NASA Solar System Exploration. (2020, 7 Oct). New Horizons: In Depth. https://solarsystem.nasa.gov/missions/new-horizons/in-depth7
The Physics Classroom. What is a projectile? (n.d.) https://www.physicsclassroom.com/Class/vectors/
Schroeder, Daniel V.Newton'southward cannon (2020, 20 January). https://physics.weber.edu/schroeder/software/NewtonsCannon.html
Sellers, Jerry Jon. (2005). Understanding Space: An Introduction to Astronautics, 3rd edition. McGraw-Hill.
Source: https://oer.pressbooks.pub/lynnanegeorge/chapter/chapter-2-orbit-geometry/
0 Response to "The Change of the Shape of Earthã¢â‚¬â„¢s Orbit From Circular to Elongated and Back Again:"
Post a Comment